カテゴリー: 数理のバミューダトライアングル

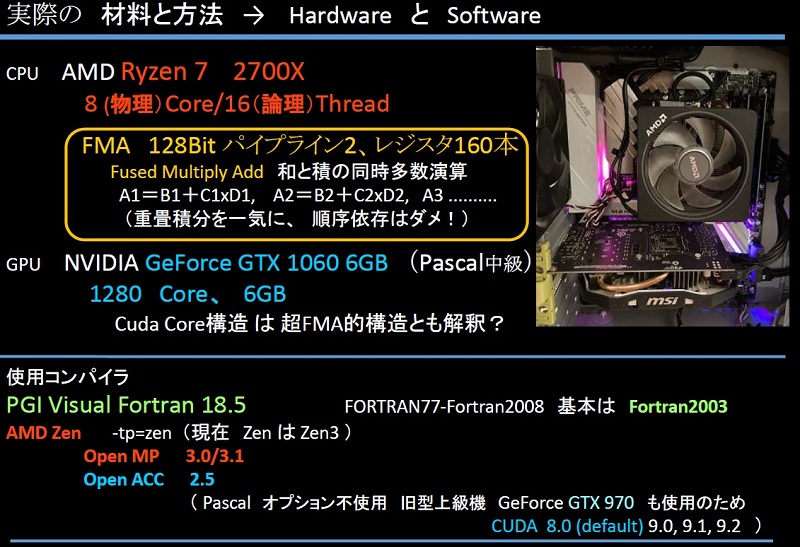
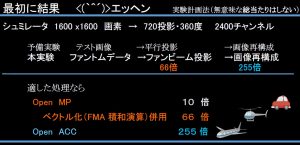
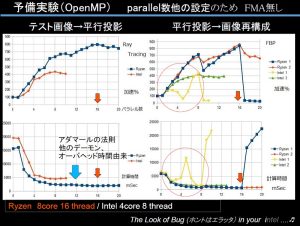
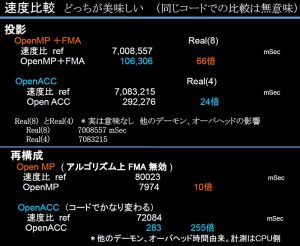
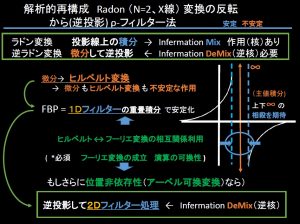
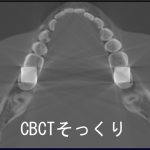
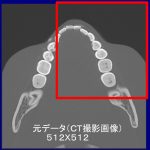
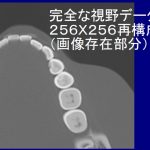
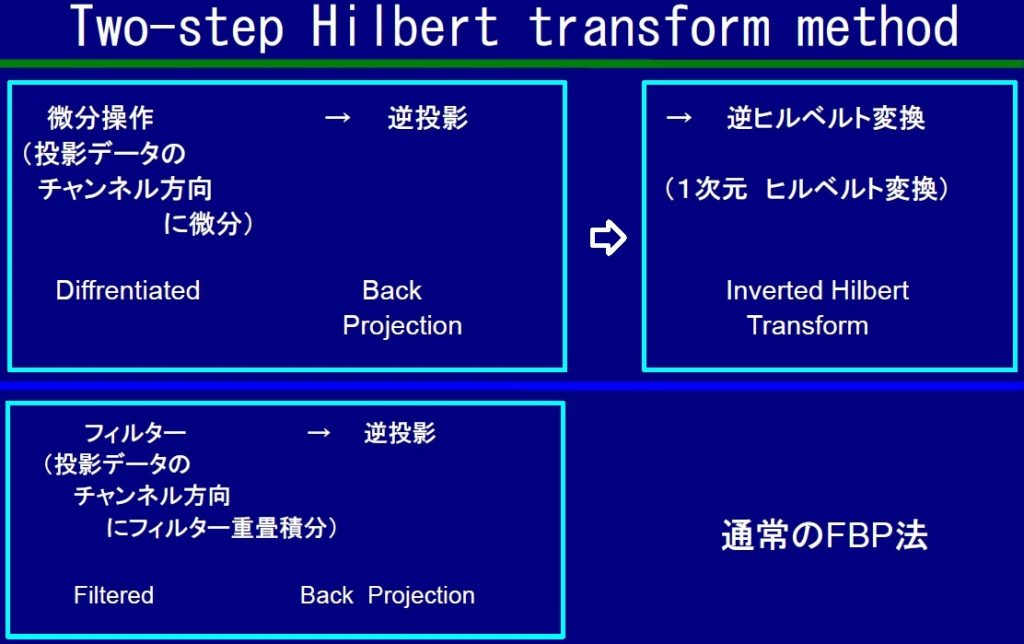
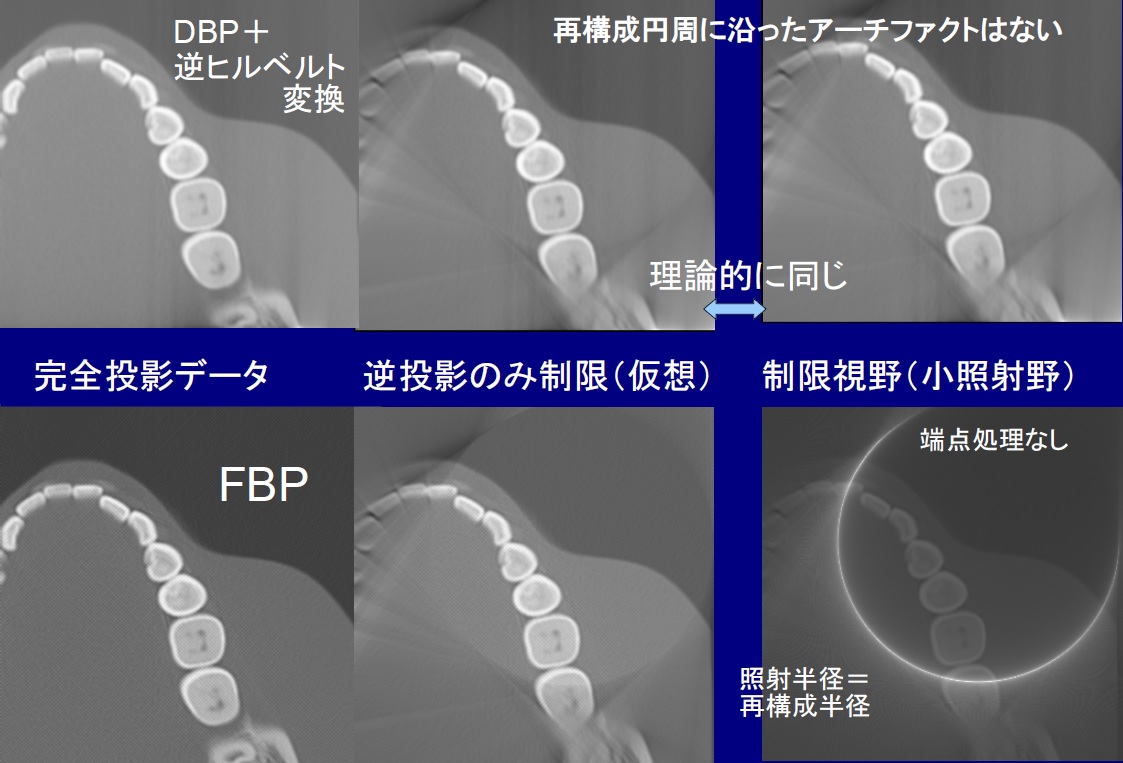
1年ぶりくらいの発表。かなり毒があるけど、やたら”３Ｄ”ＣＴと喧伝する歯科用ＣＴの現状で混乱は避けたいのでワクチン？

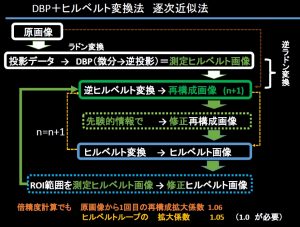
CTの再構成について臨床側にはかなりの誤解がある。数学的原理と、実際の機構や投影測定時の雑音などに対する安定性の要求からなされていることがごちゃごちゃだ。これらは、わからなければ、例えば簡単にネットなどで検索できる。CTでノーベル賞を受賞した CORMACKの受賞講演（EARLY TWO-DIMENSIONAL RECONSTRUCTION　AND　RECENT TOPICS STEMMING FROM IT,Nobel Lecture, 8 December, 1979　by　ALLAN M. CORMACK)等を読めばそれでいいし、専門外には困難かもだが、有名な物理学会誌の2つの論文読めばいい。それでも無理なら潔く混乱・誤解の元を作らず、メーカー技術者に依頼するのが良い。無論一般臨床には不要かもだが、画像専門家としてCTについて講義したり講演したりするのなら最低限のマナーでは？推薦してる本はもう理工系ではいまさら学会発表？の”フーリエ解析入門　プリンストン解析学講義１　エリアス.M.スタイン　ラミ.シャカルチ　訳 新井仁之 杉本充 高木啓行 千原浩之　日本評論社　東京”

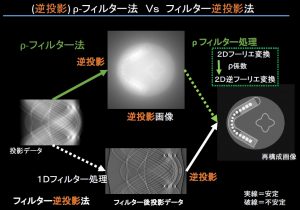
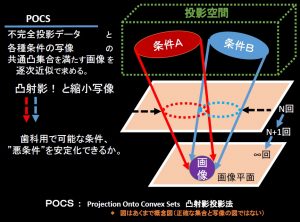
ＣＴは360/180度方向の全周全体の投影データがあれば数学的に、、はよく散見されるマチガイである。2次元では数学的にはドーナッツ🍩型でも切ったケーキ🍰型でも可能。蚊取り線香のように外から再構成の説明

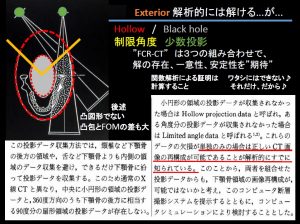
ただし測定誤差に大変弱いので、実際には機構面からも容易な全周の全体を投影する必要がある。コ―マックは最初の論文はドーナッツ🍩型、で安定しないとの批判で次は視野全円〇のスキャンを報告した。ほかにも間違いは多い。要するにCT投影・画像再構成はなんでもかんでも360/180度のラドン変換・反転に帰着ではないのだ。ただここではいわゆる不完全投影はあまり触れない。

さてよくある線形代数的解法。２Ｄの普通の再構成ですら容易ではない。

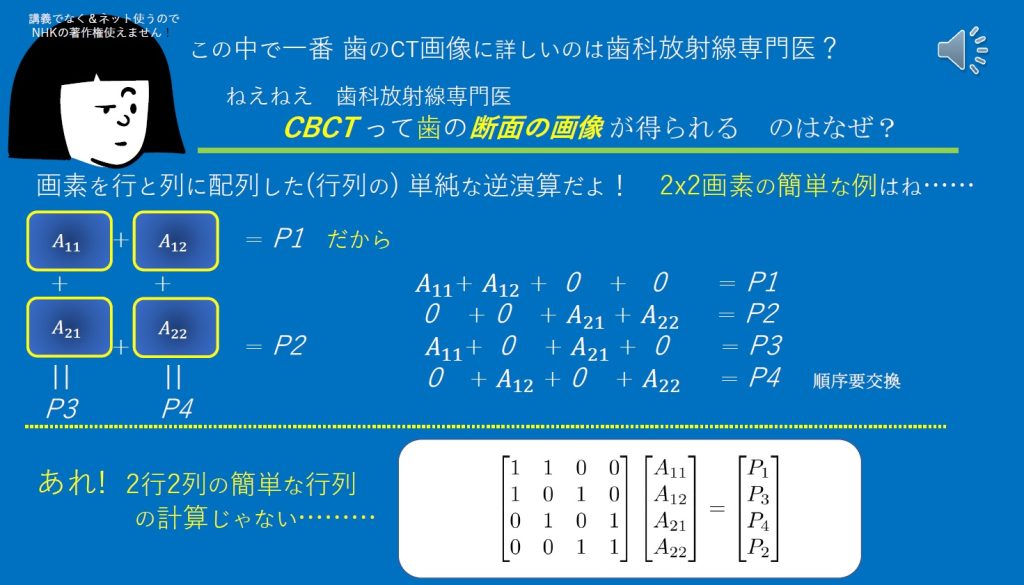
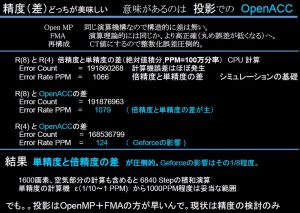
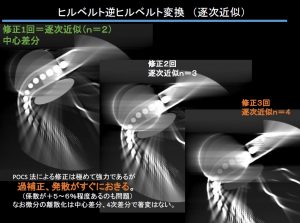
これ一見、巨大な疎行列でも帯行列に、、、なってくれないのです。ですから計算にはCT投影の性質使った今では定番の配列と計算の圧縮が当然必要です。私の学位になった研究でも大変（あんまり数学では困るという査読の方が面倒でしたけど）でした。今ならLAPACKの拡張に帯行列でないのもありますが。

フーリエでのすこしごまかし？説明？答弁？投影はそもそもフーリエ変換ではないので2次元平面というかなり幸運な場合ですら？

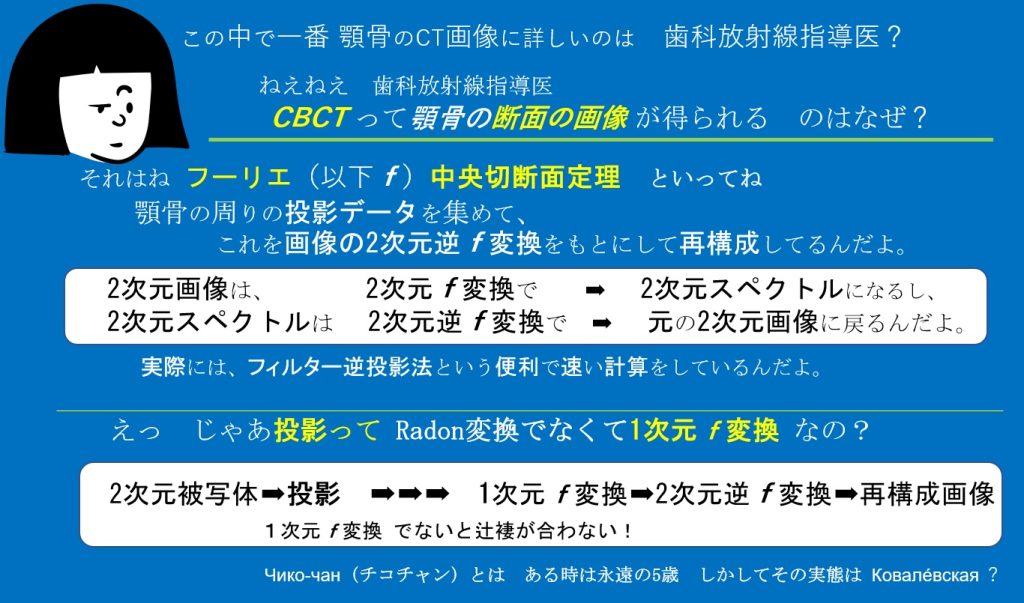
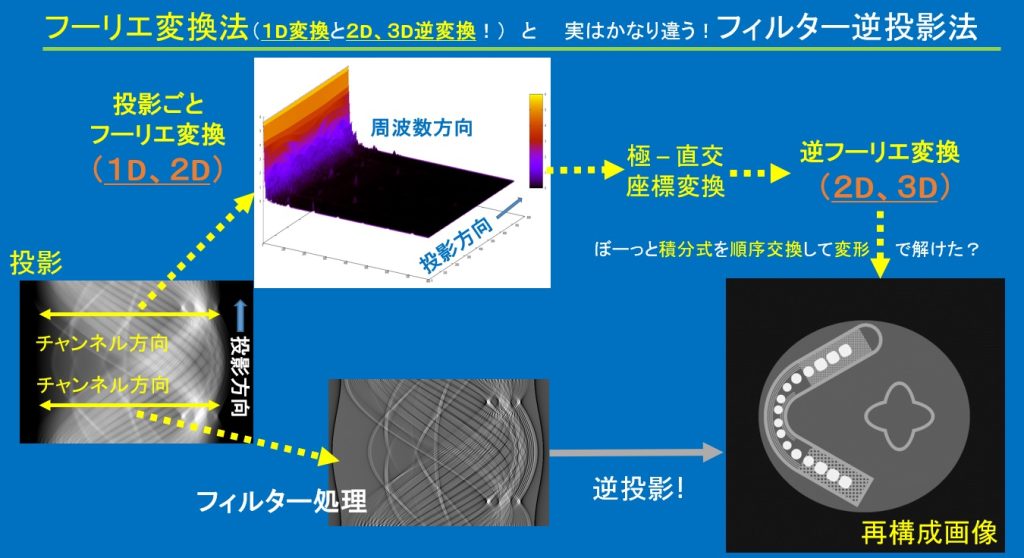
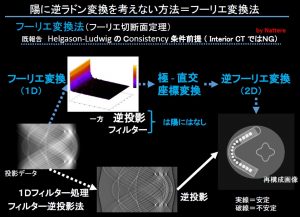
”回転しながら投影するラドン変換”はフーリエ法では極座標-直交座標変換の問題（単なる変換誤差ではない不連続点ギッブス現象など）などイロイロあるが、特に重要なヘルガソン条件でみると

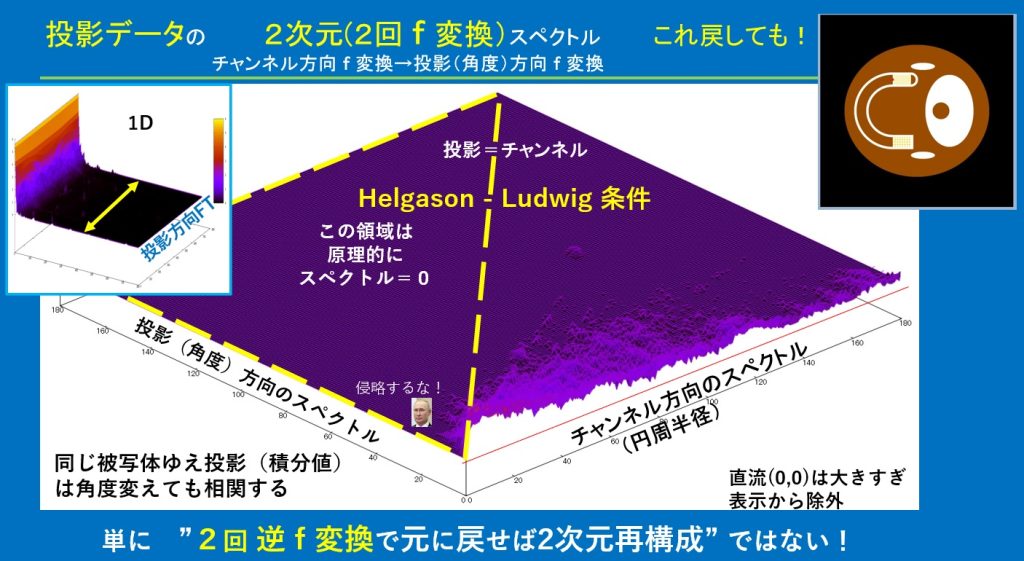
だから、CT再構成においてフーリエ切断面定理は、うるさく言うと

しかもラドン変換はそもそもn次元の被写体をn-1次元の投影積分するもの、画像再構成の反転公式もn-1次元の積分投影からn次元を再構成するもの。ゆえに2次元画像は経路に沿った1次元の投影積分データから再構成される。一方フーリエ法は1次元フーリエで多数方向から被写体ｎ次元フーリエ空間を埋める。（説明ではよくフーリエ変換とラドン変換が都合よく混合されているが、実際の研究者や講義する教員や講演者でない、学生など向けのわかりやすい解説のためなら無論それもあり。）（きちんとした参考書はたとえばThe Radon Transform and Some of Its Applications, Stanley.R.Deans, Dover, New York, 2007　この本1983年から2回も復刊された名著。今はたったの17ドル95セント！95銭と！）。

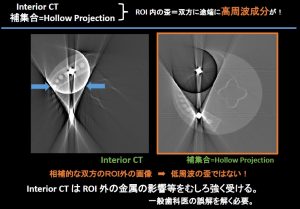
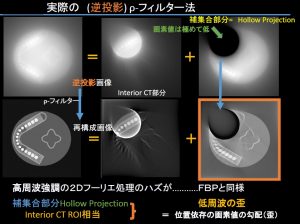
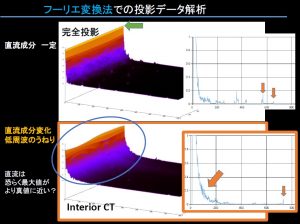
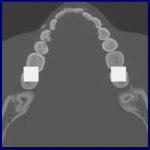
しかし巷の3次元ばやりで浮かれると、大変な被曝の増加とそれに見合わない効果しか得られない。要するに臨床では、被曝低減のため、できるだけ（雑音などに対処しながら）過剰条件よりも必要十分条件側の投影で済ませたいのだ！おまけにX線減弱は単なる引き算でなく、対数というとても厄介な性質がある。地に足のついてない酔っ払い3次元の喧伝では患者は困るのだ。きちんと被曝と画質の検討が数学的に要求される。

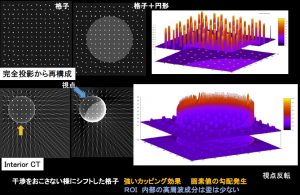
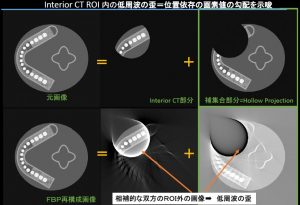
ラドン変換からの”基本的”n=3次元画像再構成では全球上のn-1=2次元の平面の面積分からの反転となり、そもそも例えばフラットパネルのような2次元位置データを持つ検出器の投影データからではないのだ！つまりホントは現在のＭＤＣＴといえども、ほとんどラドン変換からみたら2次元の積み重ねでしかない。そして被曝低減からはこれが正しい。厳密解の無い単一円周軌道コーンビームCTの現状はこの近似フェルドカンプ解。（再度強調するとフーリエ法は1次元フーリエで多数方向から３次元フーリエ空間を埋める。）いずれにしても厳密解の存在する軌道は単一ではない。また被曝量は大きく異なる（X線減弱は指数・対数でありそのままでは線形ではない！）。

まあ、聴衆やメーカーを忖度期待で見くびって勉強しないで上から目線はダメだぞ！とシロートが勉強しないで上から目線で発表したから、数学者には怒られるだろうな。(;´д｀)トホホだけど、でもたぶん副題　”車輪の再発明 は恥？だが　役に立つ！”　CORMACKはノーベル賞講演で先行数学研究をレビューしてそのフェアな姿勢は高く尊敬のマトになってきた。

Fourteen years would elapse before I learned that Radon had solved this problem in 1917.

なおチコチャンの替わりにコワレフスカヤ！にご登場願いました。

うーん、FMA の効果と思っていたけど、その後のプログラミングからは、SIMD の効果｛FMA 効果ならMP分（Max.≒10）x2倍なんで実際の66倍より少なすぎる！｝とした方が用語的にはタダシイようだ、もっと具体的にAVX128かな？。題名訂正。Ryzen7が発売になったので、マルチコアの威力。あとPCを買ったのか2018年だったのでまだGeforceが馬鹿高でなかった。まあその前が970だったけど退職して貧乏なんで1ランク下の1060でした。

かなりはやくなった。

でも、OpenMP、OpenACC でよく言われるディレクティブを追加式ではダメ。完全に書き換え必要。でも退職後で以前のコードで知財権とか言われたくないのでどうせコードは書き換えるつもりだった。まあFORTRAN77・Fortran90　もいい言語だけど、modern fortran　移行も必要だし。（なおSIMDはやはりCの方がコンパイラだのみでソースコード直してしてはお願いの fortran より直接細かい制御できるので向いているよ～だ。でも大変みたい。）

予備検討。やはりRyzenは凄い

かなり重たいファンビームの実験。無論単純な画像のレイトレーシングではない。ファントムの元素の減弱係数はNISTに、エネルギーは10keV~120keVまで、0.1mm画素サイズ、0.05mmステップ、1600×1600画素720投影。2400チャンネルに1チャンネル3本の光子。セプターの考慮でパッキングレシオ75％、出力は870Mバイトもある。

投影はデーター重さからGefoceが振るわない（レイトレーシングコアもない機種だし）一方再構成はGeforceおそるべし。

まあ精度は、単精度倍精度が支配的なのは当たり前のこと。

 

女刑事と殺人鬼？が入れ替わるとドラマになるのだが、、、
よろず演算は可換と勝手に決めている愚民のなんとオオイことか！
ハタと各種のCT画像再構成は逆ラドン変換を構成する3つの要素（微分、逆投影、逆ヒルベルト変換）の可換性が前提と気づく。綾瀬さんのドラマは脚本もいいな！
で学会で発表した。スライドのPDFの切り取りで画像小さい。

歯科で言う”小照射CT”＝Interior CTの問題は数学的な補集合の解析が必要。この補集合=Hollow Projectionは実は、Interior CTと異なり、逆に数学的には完全な再構成が可能。昔々のこれにスガッタ私の論文。

（無論、実際は誤差で逆に酷いことに、ノーベル賞貰ったコーマックの最初の論文がそれで非難された。で2つ目の論文では現在の投影）

さてCT画像再構成についてラドン変換系と直接フーリエ系に大別してみる。
さらに演算の可換性があるなら、ラドン変換系では、逆投影の位置を変えた再構成が可能。ここではρフィルター法を。

ラドン系と、逆投影を陽に行わない、フーリエ系での解析も合わせてようやく、数学的な解析ができる。

*ヒルベルト変換は周期的電気信号の変化が振幅の変化なのか位相の変化なのかをみる”解析信号”で電気系ではよく出てくるが画像系ではなじみがない。でも調べれば山ほどイロイロですね。このようにフーリエから符号関数を経由して定義する場合もあり、フーリエ系の教科書には。

まず最初にFBP法による問題を、幾何学図形で示す。

ついでInterior CTと補集合Hollow Projection。

いずれも完全な再構成ができるならば、それぞれのROIのみに画像ができるはずである。無論そうはならない。補集合のHollowProjectionに本来ないはずの低周波数の歪があることがはっきり認められる。Interior CTでは構造によりマスクされ視覚的にはわかりにくい歪が補集合側で負に明示されている。

今度は（検出感度に下限設定）アーチファクトのある状態。

歪は双方かつ低周波のみではないことが明確である。

いよいよ重要な作用素の可換性について検討する。
逆投影作用を重視すると、FBPと逆投影作用素の位置が前後するρフィルター法による解析になる。

模式図と中間過程で違いを示した。

さて実例

逆投影では本来０であるべき補集合での部分はほぼ予想されるように低い値。一方ρフィルターの適応後では本来の作用である高周波での回復でなく低周波の歪が明白。やはり位置非依存と仮定して参照体で画素値の分析や補正は困難なのだ。

ついで陽にラドン変換を考えずにフーリエ変換のみの場合。
本来ルードリッヒの一致条件の成立が必須なので本来はNG。）


それゆえやはり投影データでは基本となり唯一の値であるはずの画像直流成分がうねる！のみならず低周波成分の盛り上がりが顕著。やはり画素値の分析や補正は困難。

補集合部分には位置依存性の濃度勾配が見らる。またフーリエ法は既知のごとく周期雑音酷い。

さて、いよいよ微分逆投影逆ヒルベルト変換法のシミュレーターの実装。Fotran90でコード。前回のある学会で提案したチンレスト（顎押さえ）と口腔内参照体でヒルベルト線をカバー。ここらの仔細は質問もあったので、次回発表しよう。
まずは、この先験的データを用いない＝逐次近似をしない、1回の微分逆投影逆ヒルベルト変換法。ROIについては、完全投影とInterior CTとなる。補集合部分は無論論理的には再構成できないので。

カッピング効果は明らかに少ないようですね。一方、完全投影では演算範囲の長いフィルターBPより劣り、Interior CTでは演算範囲の狭い微分（離散系では差分）なんでカッピング効果が少なくて良いという数学的性質が明確に。

本番は、この既知情報を用いた逐次近似法。
逐次近似は一般的なPOCS法。
ただ、Interior CTでは単位円にのみ画像があるという条件は成立しない。

で追加の先験的情報の設定。辺縁の安全域は１０％設定
逐次近似では系の安定性が問題たが、やはり倍精度でも５％程度に抑えるのが限界。(これは離散系では特異値処理が困難であることからだろう。）

最後の逐次近似の結果。

逐次近似どころか1回の補正のN＝２でここまで。しかしPOCS法は極めて強力であるが、やはり強力さに常に相反する過補正や発散がすぐ起きるので対策が必要なよう。

そもそも、最初は核医学でSPECTをテーマにしていたが、歯科での核医学設備の維持は2重投資で先はないと。やはりFCRやCTがせいぜいと思っていた。そこでFCR利用して歯科用CT。ただし研究はほとんど数学。当時はEM法などは医科でも未知の世界。IEEEが頼り。歯科医より数理したかったのでこれ幸い。

原点の歯科用CT実験機

フラットパネルディデクターの無い時代なんでFCR利用。最初の頃、再構成にかかる時間は、FCRの12インチ！の光ディスクを共同研究者の富士フィルムA研究所に送り、磁気テープに変換。これを送ってもらい、鹿児島大学総合計算センターにもっていってIBMメインフレームで読み取り変換（できるので伝説的に有名な女性技官の方がその場でFortranプログラムで唖然！）、これをPCH98（やむなく私物でした！）で前処理して、1昼夜逐次近似（EM）法ですね。ほぼ1週間！

かなりの額の科学研究費6年近く頂いた。でも応援してくれる側と学内機構でもうグチャグチャ。最後の試験研究は額が大きいのと（実質個人研究では学内最高額）、面白しろそうだったのか、会計検査院本省から査察にくると内示もあり、若い女性の係官（初めての仕事だったそうだ！まあ手ごろなんでしょう！好意的でした）が指導？の上司と調べにきた。産学連帯のいまなら超もてはやされてだろな。。当時は、国費の科研費で特許をとるな！と厳命された時代。（これ完全に特許成立する内容！）

　 

成果は北米放射線学会で採択なんで展示！あれ発表旅費は採択のワタシが貰うはずなのに！ヽ(`Д´)ﾉﾌﾟﾝﾌﾟﾝ。親分が私費でいくんならとOKなんでその後1週間シアトル～カナダでのんびり遊んできました。当時の超多忙な医局ですが、誰も文句なし。

 

現在の被曝もアーチファクトも多い、なんのことはない、あるフラットパネルディデクターにあわせた歯科用CT軌道でなく2×8㎝の顎骨軌道。これは現在に至るまでワタシしか成功していない。。けど。。スライスは1mm画素だもんね。。（当時のCTは2mmだったんのでその上ということで、(⌒▽⌒)アハハ!）

ところがあっという間に海の向こうでSPIRAL-CTが実用化。おまけに歯学部世界初の導入が決まり、てんてこ舞い。（同時期にその凄さ見抜けず導入しなかったところは悲惨）ただ、同時にその凄さみてると、お話になりません。これは白旗。その後北大、医科歯科により高性能機が導入。今ではSPIRALでないCTはあるのかしらん。。

後日談。CT導入後安定したら開発元のドイツへ留学。研究と臨床で絶対に必須。（実際に多くの成果が上がった！）。無論、導入の利益誘導では困るので正攻法の文部科学省の留学。ところが学内選考、文部科学省選考OKで決定！なのに1名学内の担当者がギャーギャー（この権限もないはずの担当者の思い込みを抑えられない大学の統治機構はいかがなもの。これが当時の大学村！このご老人、大英博物館に留学決定の先生に、大英博物館は入場料とるから駄目だ！とまたいやがらせ。教員にイチャモンつけるのが生きがいの職員、技官の典型だが、本人はいたって規則順守？の正義に酔ってた！大学・公務員改革はある種はやむなしだったかも。）

制御は最新の16BitPC-ATと新たなOS、Windows　でした！