かつて制限視野(小照射野)CTの問題に、投影データを偏微分し逆投影し”Hilbert画像”を再構成し、次に画像に逆Hilbert変換を行う方法を検討した。無論、当時の詰めはあまく、一部のみ。
CTは、投影(Radon変換)から、画像再構成(逆Radon変換)する。
逆Radon変換では投影データのチャンネル方向の偏微分をHilbert変換し、逆投影する。この厳密解法は特異点があり解の安定性やコーシ主値積分に問題がある。
通常の完全な投影データ(実は冗長)に対しては、偏微分とHilbert変換を1回の演算でおこなうフィルター逆投影(FBP)法が確立。
まずはコンピュータシュミレーションの蓋然性確認。ファントム(模型)画像に金属をおいたもので、アーチファクトの再現
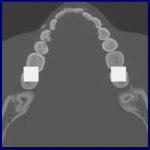
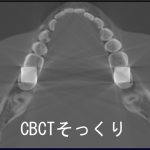
視野の切り出しや制限投影
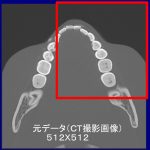
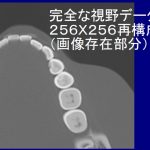

逆投影の制限でなく、制限投影(小照射野)=両端のデータもないとフィルター操作に大きな支障が生じる。画像の劣化は甚だしい。

さてNooらにより、不完全投影データに対してTwo-Step Hilbert 変換法が導出されている。ROI-再構成に完全投影は不要であると証明した。ただし条件がある。物体の境界の外側で0である拘束などの先験的条件である。(歯科用CTではさらに内部に既知の領域があれば、KUDOらの方法も使える。これは当時はKUDOの論文から言及のみに終わった。。ただしこの既知は幾何学性のみでなくCT値において多色X線エネルギーであるCTではなかなか容易な話ではないのだ。。)
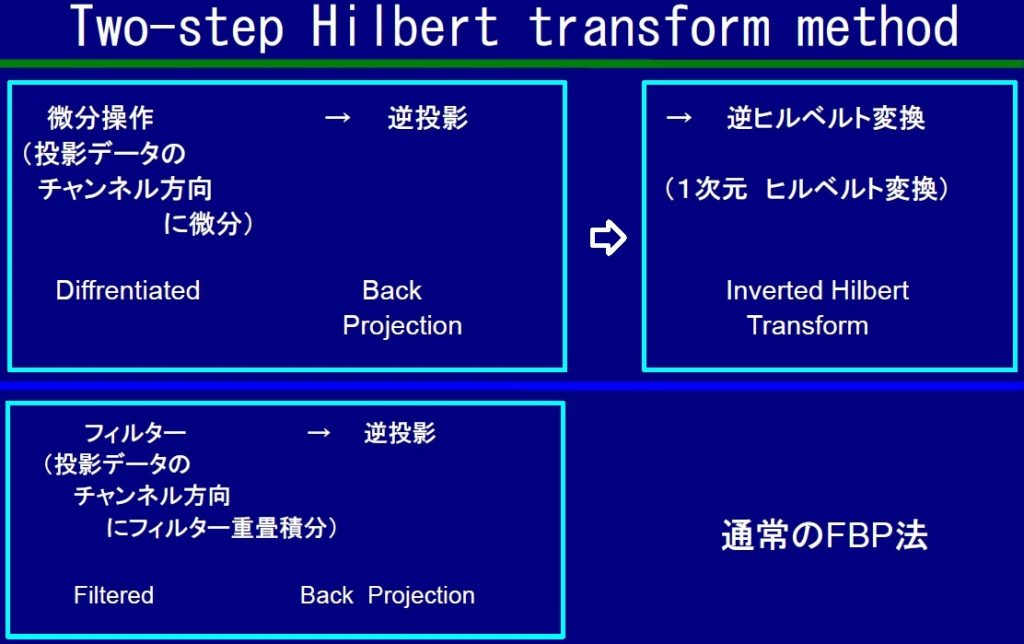
投影データを偏微分した後に逆投影(Differentiated Back Projection)し、”Hilbert画像”を得る。ついで画像に逆Hilbert変換を行う。順序がポイント。


この補正項Ctの計算とか本来逐次近似の部分なんかを当時はえいやっと。きちんと計算する方法や、逐次近似法を考えるべき。画像には明らかに演算による方向依存性が!
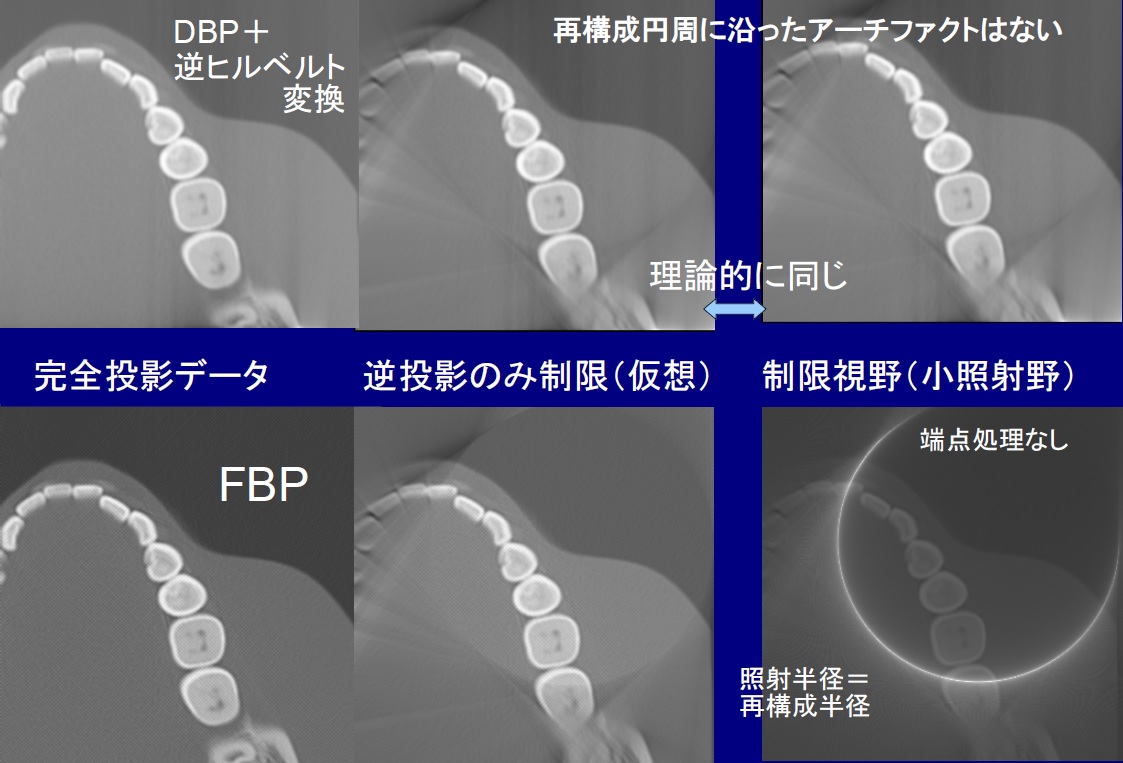
完全な投影データ(冗長)ではFBPに画質は優れ実用的に問題はない。一方データに制限が加わった場合のロバスト性は現状でもこの方法が明らかに高い。

漂着しました。
小照射野辺縁は、太陽圏:ヘリオポーズ(Heliopause)のように、外部の構造(画素値)を圧縮して集約しているかのようで、内部への乱流を遮っているように見えてしまいます。凪の圏内にも、外部に強力なバーストが存在したなら、ヘリオポーズを突き破ってくるのでしょうね。
追伸:漂流物二つ回収
この手の再構成には位相論と群論の2つが必要で高等数学教育受けていない私には、恐ろしくて!!。フィルター逆投影法の局所tomographyのカッピング効果はもうガミラスの遊星爆弾に見えます。InteriorCTとその補集合であるHollow-Projectionは東洋の神秘、陰陽の様です。加法群?学会終わったらまたアップします。。。
草々にレスありがとうございます。
当方、遙か昔(30年程前)
画像処理アルゴリズム (アルゴリズムシリーズ 2)
斎藤 恒雄 (著)近代科学社、ISBN-10 : 4844372130
にて、「計算機トモグラフィ」をトレース・理解後、続く「ラドン変換に基づく計算機トモグラフィの解析」・「3次元計算機トモグラフィ」を「すごい!」と眺めるだけで、ラドン変換入り口付近で止まってしまい、今に至っています。
でも、昨今、GPUを含め、コンピュータ環境が著しく良くなっていることもあり、いろいろとやってみたいことが増えてきています。
続編を楽しみにしております。
今後ともよろしくお願い申し上げます。
斎藤恒雄先生の本はボロボロになるまで読みました。研究室にうかがったことあります。数式に誤植が多くてとボヤいでおられました。今でも発表ではこの教科書引用させていただいています。
早々に「草々」と間違えて投稿してしまい、申し訳ございません。
さて「ラドン」で足を止めた私にとって「ヒルベルトって何?」状態でしたが、信号解析関連資料をざっくり眺め、思い切って太陽圏を突き破ってみる大冒険を試みてみます(間違ってたらご指摘願います)
「投影データのチャンネル方向への微分操作」
というものを考えたとき
1.チャンネル方向を角度情報と見做せば、微分操作=90度位相のずれたデータを扱うことになるので、ヒルベルト変換しているのと同等となり、Back Projection後に、逆ヒルベルト変換する。
2.チャンネル方向の変化には、Hollow-Projectionのデータも乗っかっている(投影方向が変化すると「ベース」が変動する)ので、微分(離散系では差分)操作にて、Hollow-Projectionのデータを含めた「ベース」に依存しないデータとして扱える。
の2点から捉えると、「再構成円周に沿ったアーチファクトが【なぜ】出ないのか?」とか理解しやすいように思いました。
(とんでもない勘違いをしている可能性があり、不安ですが・・・)
あと、フーリエ変換では、横軸方向での無限大のカット(打ち切り)が影響しますが、ヒルベルト変換では1/tにて、横軸=0での縦軸方向への±無限大の影響が大きいのだと思いました。
参考にした資料
https://www.murase.m.is.nagoya-u.ac.jp/~ide/res/paper/J07-symposium-hishi-1.pdf
http://www1.accsnet.ne.jp/~aml00731/c/communicate/Seminar_text.pdf
私は実は歯医者(元?もう引退してます。猫とメダカと暮らしてます)で数学はキチンと教育受けてません。マチガイ多いと思います。気が付いたら教えてください。これが前提ですが。
まず、CTのデータ収集ですが、これは極座標での投影+information-Mix作用ですね。要するに投影のとき投影線方向の距離(座標)情報がMixされていなければ、単なる回転変換なんで、再構成なんぞ不要ですね。
ですから、再構成では逆投影+information-DeMix作用があれば良いことになります。この逆投影とDeMix作用が可換で、またDeMix作用をさらに分解できれば、様々な方法が考えられます。これがラドン変換系の再構成の基礎になります。DeMixの方法を前にして、特異値(ヒルベルト変換はコーシ積分必要ですね、微分も離散系ではしにくい)を最初に滑らかにしていくのがFBPです。最初に微分、後でヒルベルト変換で、逆投影を中に挟むのがDBP逆ヒルベルト変換法ですね。
ヒルベルト変換→逆投影→逆ヒルベルト変換では可換な場合、前後で作用素、逆作用素で相殺され、逆投影のみのボケた画像になってしまいます。要するに微分+逆投影(滑らか=information-Mix作用あり)の組でヒルベルト変換+座標変換と考えた方が自然です。
Hollow-Projectionのデータはサイノグラムで明らかなようにinteriorCT投影データの補集合ですのでこれには含まれてはいません。(しかし御投稿のようにHollow-Projectionの領域の成分はinteriorCT投影データに重畳されていますね。)
つまり円周方向のアーファクトが出ないのは、最初の微分作用が、4次精度の差分でも高々2チャンネル外側までの局所の演算であり、ここを抑制すればいい!ということによります。微分ですますのは数学的には良い方法ですが、実際の誤差の不可避の検出器を使う方法では誤差への素子感度が高くなりすぎダメな話で、ここら辺は井上多聞先生が初期に鋭く指摘されていますね。(お話をきいたりお会いしたこともありませんが、数学出身で東芝から筑波大という経歴と聞いていますんでさすがですね。)
なお実は日曜日の歯科関係の学会でちょうどここらへんを発表するつもりです。発表前にあまりUpできないのでここらへんで。歯科医向けに歯科用CTのヘンテコな神話が流行ってたので心配で老婆心でイロイロ発表してきました。。
未熟なレベルでの思考に対し、非常に詳細にご教示頂きまして、有り難うございます。
「要するに微分+逆投影(滑らか=information-Mix作用あり)の組でヒルベルト変換+座標変換と考えた方が自然です」
この部分、やはり「組(セット)」なんですね。
「微分に対する積分が無い」のは何故・・・? と、不思議に思っていたところです。理解するには、やはり難しいところですね。
ところで斎藤恒雄先生の本、今見返してみたら「ラドン変換」に入ったところで天下り的に積分の式が出てきたので躓いたようです。その直後「逆問題とその解き方」岡本 良夫(オーム社)を購入したのですが、ますます分からなくなったという次第です。
「ラドン変換」(今見返してみると「回転座標系への変換だね」ですが・・・)、当時乗り越えていたら、もっと先まで理解しつつ読み進めていただろうに、と今更ながら思っています。
人それぞれに、その時々で越えられるか、越えられないかの、ほんの僅かな違いが、後々まで影響するものだと思いました。
間違ってなかったら幸いなんですが。私は数学教育受けてないので。
逆投影という訳語がいけないのかもです。これ英語ではInvertでなくBackなんで逆作用素ではないのですが、あたかも逆の演算のように思いがちです。投影も、逆投影も要するに滑らか=information-Mix作用ありなんですが、逆だと回復のinformation-DeMix作用のようにとられますね。なお、岡本先生の本は線形代数の本なんで最初に少しCTありますが、ラドン変換は詳しくないと思いますね。和書にはなかなか良い解説がないですね。一方ナタラーの教科書はSIAM(米国工業並びに応用数学会叢書)にも収載されてますね。収載まえの単行本、滅茶苦茶高かったのですが持ってますが、、こっちは誤植が多くて、、)
おはようございます
「なぜ、そうなるのだろうか?」という素朴な疑問と興味から沸き起こる「知りたい、分かりたい」ということは、人類にとって尽きることのない基本的な欲求なのでしょうね。
確かに「和書にはなかなか良い解説がない」ですね。
やはり難しい理論を理解するには、実際に動かしてみるしかないのでしょうね。YM-Lab先生が提示されておられるような画像を、(無論、入門用無料版と研究用有料版など分けて)誰でも気軽にシミュレートできるようになるのが良いようにも思えました。
こちらのサイトでそのようなシミュレータがアップされることを期待しております。もしアップされたなら、有料版を購入したいと思っています(無論、理解したいために支出した膨大な書籍代と比較するなら、大したことのない額であれば・・・ですが・・・^_^;)
明日、関連学会でご発表されるとのこと。学会関係もコロナで大変な状況かと思われますが、YM-Lab先生先生にとっても、聴衆の方々にとっても、有意義な時間となりますことを祈念いたしております。
たまたま漂着した旅人に対し、詳しく、かつ、ご丁寧に、ご教示いただきましたこと、深謝いたします。
ありがとうございました。
公開についてはA)研究者、学制さんに個別に提供。B)無償公開。C)有償公開。の3つがあります。
Aはすぐできて簡単ですね。マニュアルや利用規約を作る必要はありませんね。もっともすべてFortranで書いてあります。このコンパイラやMS-VSーStudio使えるのが大前提です。
B)はマニュアル作ったり、規約きちんとしないと盗用投稿、バグ責任、イロイロで第3者に迷惑かけてしまいます。昔まだグラボなかったころに高度な3DをFortranで書き公開しようとしたときプロ(今では定番の1つの会社!)から学会で教えてもらいました。医療関係では絶対必須ですね。その後この手の話(薬機法や治験規則違反の要求!)で実は臨床では大変迷惑してきました。私のデータはファントムつまり人体ではなく樹脂に包埋した標本骨か数値ファントムでCT装置点検等の流用の範囲です。しかし正規手続きなしに医療用装置で大量の実験やしまいに人体データを入れる輩が絶対でてきますね。(コロナ騒動と同じで地位や学歴と倫理観は無相関です!)
C)はさらに厄介です。単にソフトだけでも筑波大学で工藤教授(斎藤先生の助教授だった方)がヒルベルト変換の一部には特許権もっておられます。PDF自体は有償にできても、シミュレータにして実態をつくり、有償にはできませんね。無論特許権は金銭伴わない実験や研究自体は対象になりませんから、無償で勉強用はもんだーいなし♪!ですね。
なお実はこのページは、知財権ややこしいと困るので、2004年頃の10年以上前のデータと結果なんです。。。新しいと流用や最悪、コピペして論文書かれると査読者とか編集者に迷惑かけるので。。でオリジナルの2004年の論文を明記して数式をコピペして、オリジナルから読んでいただこうと。。(⌒▽⌒)アハハ!