女刑事と殺人鬼?が入れ替わるとドラマになるのだが、、、
よろず演算は可換と勝手に決めている愚民のなんとオオイことか!
ハタと各種のCT画像再構成は逆ラドン変換を構成する3つの要素(微分、逆投影、逆ヒルベルト変換)の可換性が前提と気づく。綾瀬さんのドラマは脚本もいいな!
で学会で発表した。スライドのPDFの切り取りで画像小さい。
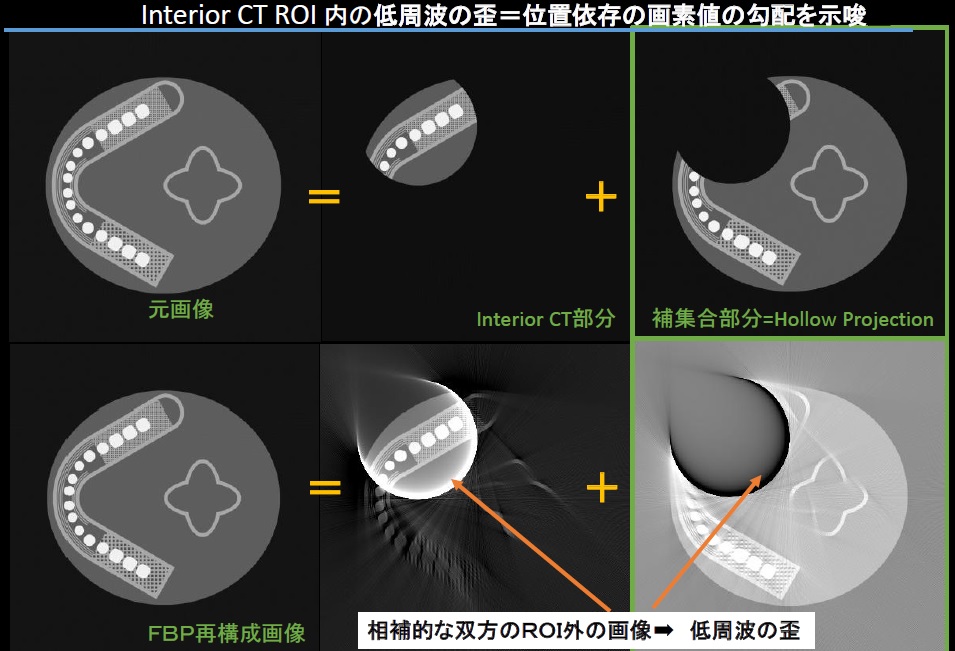
歯科で言う”小照射CT”=Interior CTの問題は数学的な補集合の解析が必要。この補集合=Hollow Projectionは実は、Interior CTと異なり、逆に数学的には完全な再構成が可能。昔々のこれにスガッタ私の論文。
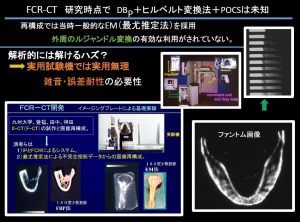
(無論、実際は誤差で逆に酷いことに、ノーベル賞貰ったコーマックの最初の論文がそれで非難された。で2つ目の論文では現在の投影)
さてCT画像再構成についてラドン変換系と直接フーリエ系に大別してみる。
さらに演算の可換性があるなら、ラドン変換系では、逆投影の位置を変えた再構成が可能。ここではρフィルター法を。
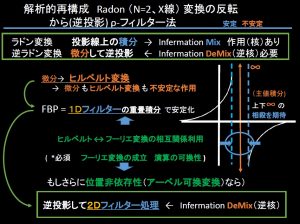
ラドン系と、逆投影を陽に行わない、フーリエ系での解析も合わせてようやく、数学的な解析ができる。
*ヒルベルト変換は周期的電気信号の変化が振幅の変化なのか位相の変化なのかをみる”解析信号”で電気系ではよく出てくるが画像系ではなじみがない。でも調べれば山ほどイロイロですね。このようにフーリエから符号関数を経由して定義する場合もあり、フーリエ系の教科書には。
まず最初にFBP法による問題を、幾何学図形で示す。
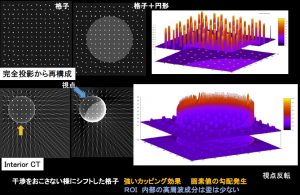
ついでInterior CTと補集合Hollow Projection。
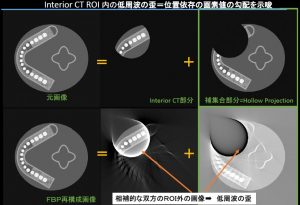
いずれも完全な再構成ができるならば、それぞれのROIのみに画像ができるはずである。無論そうはならない。補集合のHollowProjectionに本来ないはずの低周波数の歪があることがはっきり認められる。Interior CTでは構造によりマスクされ視覚的にはわかりにくい歪が補集合側で負に明示されている。
今度は(検出感度に下限設定)アーチファクトのある状態。
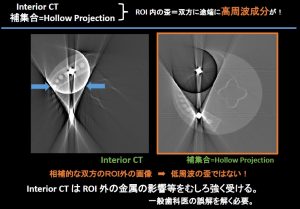
歪は双方かつ低周波のみではないことが明確である。
いよいよ重要な作用素の可換性について検討する。
逆投影作用を重視すると、FBPと逆投影作用素の位置が前後するρフィルター法による解析になる。
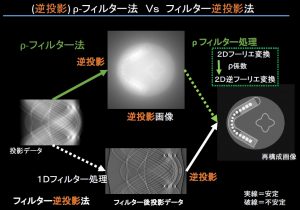
模式図と中間過程で違いを示した。
さて実例
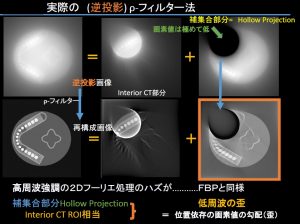
逆投影では本来0であるべき補集合での部分はほぼ予想されるように低い値。一方ρフィルターの適応後では本来の作用である高周波での回復でなく低周波の歪が明白。やはり位置非依存と仮定して参照体で画素値の分析や補正は困難なのだ。
ついで陽にラドン変換を考えずにフーリエ変換のみの場合。
本来ルードリッヒの一致条件の成立が必須なので本来はNG。)
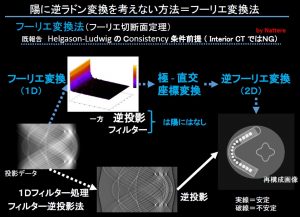
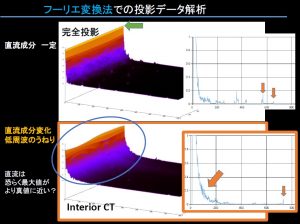
それゆえやはり投影データでは基本となり唯一の値であるはずの画像直流成分がうねる!のみならず低周波成分の盛り上がりが顕著。やはり画素値の分析や補正は困難。

補集合部分には位置依存性の濃度勾配が見らる。またフーリエ法は既知のごとく周期雑音酷い。
さて、いよいよ微分逆投影逆ヒルベルト変換法のシミュレーターの実装。Fotran90でコード。前回のある学会で提案したチンレスト(顎押さえ)と口腔内参照体でヒルベルト線をカバー。ここらの仔細は質問もあったので、次回発表しよう。
まずは、この先験的データを用いない=逐次近似をしない、1回の微分逆投影逆ヒルベルト変換法。ROIについては、完全投影とInterior CTとなる。補集合部分は無論論理的には再構成できないので。

カッピング効果は明らかに少ないようですね。一方、完全投影では演算範囲の長いフィルターBPより劣り、Interior CTでは演算範囲の狭い微分(離散系では差分)なんでカッピング効果が少なくて良いという数学的性質が明確に。
本番は、この既知情報を用いた逐次近似法。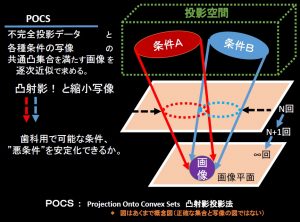
逐次近似は一般的なPOCS法。
ただ、Interior CTでは単位円にのみ画像があるという条件は成立しない。

で追加の先験的情報の設定。辺縁の安全域は10%設定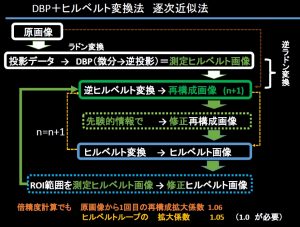
逐次近似では系の安定性が問題たが、やはり倍精度でも5%程度に抑えるのが限界。(これは離散系では特異値処理が困難であることからだろう。)
最後の逐次近似の結果。
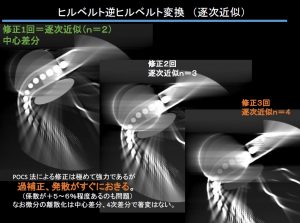
逐次近似どころか1回の補正のN=2でここまで。しかしPOCS法は極めて強力であるが、やはり強力さに常に相反する過補正や発散がすぐ起きるので対策が必要なよう。